Elektrische Kabel, der Gartenschlauch oder die Lichterkette, sie alle haben eine Eigenschaft gemeinsam: Sie verknoten sich ständig scheinbar ohne äußeres Zutun zu einem schier unentwirrbaren Knäuel. Aber wie? Ein amerikanischer Forscher hat nun erstmals ein Modell dieser rätselhaften Knotenbildung entwickelt und berichtet darüber in der Fachzeitschrift „Proceedings of the National Academy of Sciences”.
„Knotenbildung ist für viele Bereiche wichtig”, erklärt Douglas Smith, Assistenzprofessor für Physik an der Universität von Kalifornien in San Diego und Seniorautor der Studie. So bilden sich zum Beispiel Knoten auch in der DNA, die ja auch ein fadenähnliches Molekül ist. Zellen besitzen Enzyme, die diese Knoten wieder auflösen, indem sie die DNA schneiden. Einige Wirkstoffe aus der Krebstherapie nutzen dies aus und hindern die Krebszellen am Entknoten ihrer DNA.“ Initiiert wurde die Studie allerdings von Dorian Raymer, einem wissenschaftlichen Mitarbeiter von Smith, der sich speziell für die Knotentheorie interessierte. Dabei handelt es sich um einen Zweig der Mathematik, der Formeln einsetzt, um verschiedene Knoten voneinander zu unterscheiden. Ihm fiel auf, dass eigentlich niemand so recht wusste, wie Knoten sich eigentlich bilden.
“Es ist bisher nur sehr wenig experimentelle Arbeit durchgeführt worden, um die Knotentheorie auf Analyse und Klassifikation von echten, physikalisch existierenden Knoten anzuwenden“, so Smith. „Für Mathematiker ist das Problem eher abstrakt. Sie denken sich mögliche Knotenformen aus und klassifizieren sie. In unseren Experimenten erzeugten wir tausende unterschiedlicher Knoten und nutzten dann die mathematische Knotentheorie, um sie zu analysieren. Daraus entwickelten wir ein einfaches physikalisches Modell, dass unsere Ergebnisse erklären kann.“
Schnurstücke in sich drehender Plastikbox
Die Experimente bestanden aus einer Plastikbox, die durch einen computergesteuerten Motor gedreht wurde. Ein Stück Schnur wurde hineingeworfen und darin wie Kleider in einem Wäschetrockner umhergewirbelt. Sehr schnell, schon innerhalb von zehn Sekunden, bildeten sich die ersten Knoten in der Schnur. Die Wissenschaftler wiederholten das Experiment mehr als 3.000 Mal und variierten dabei die Länge und Steifigkeit der Schnur, die Größe der Box sowie die Geschwindigkeit der Drehung. Anschließend klassifizierten sie die entstandenen Knotenformen.

„Es ist nahezu unmöglich, unterschiedliche Knoten allein durch Anschauen zu unterscheiden”, erklärt Raymer. „Deshalb entwickelte ich ein Programm dafür. Der Computer zählt jede Kreuzung des Fadens und registriert, welcher der beiden Schnurbereiche oben liegt und in welche Richtung er weiterläuft. Das Ergebnis besteht aus einer Reihe von Zahlen die in eine Art mathematischen Fingerabdruck für diesen Knoten übersetzt werden kann. Dabei nutzten wir das Jones-Polynom, eine berühmte, von Vaughn Jones entwickelte mathematische Formel, die auch Knoten erkennt, die zwar auf den ersten Blick verschieden aussehen, aber eigentlich identisch sind.“
Knotenvielfalt wie in der Theorie vorhergesagt
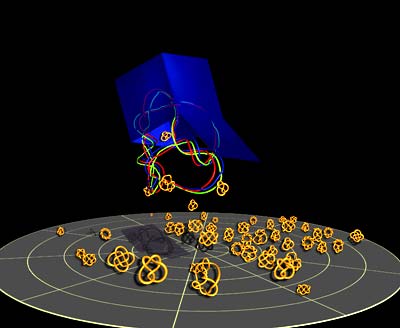
Und das Ergebnis war erstaunlich: Anstatt nur wenige Arten von Knoten zu bekommen, erhielten Smith und Raymer alle Formen, die die Mathematik theoretisch postuliert hatte, zumindest bis zu einem bestimmten Niveau der Komplexität. Je länger die Schnur, desto größer war die Wahrscheinlichkeit, komplexere Knoten zu erhalten. Basierend auf diesen Beobachtungen entwickelten die Forscher ein vereinfachtes Modell für die Knotenbildung.
Nach diesem spielt sich dabei Folgendes ab: Zunächst bildet die Schnur konzentrische Schlingen, wie ein aufgerollter Gartenschlauch. Ihr freies Ende bewegt sich durch diese Schlingen mit einer jeweils rund 50prozentigen Wahrscheinlichkeit unter oder über eine Schlinge hinweg zu gehen. Aus dieser einfachen Abfolge von Bewegungen resultiert, das zeigte eine auf diesem Modell beruhende Simulation, tatsächlich ein Muster aus einfachen und komplexen Knoten, das dem in den Experimenten erzielten gleicht.
Nach Ansicht von Smith enthüllen ihre Ergebnisse zwar keinen magischen Trick, um eine Knotenbildung zu verhindern, aber sie geben einen hoffnungsvollen Ansatz für junge Wissenschaftler: „Selbst heute gibt es noch interessante wissenschaftliche Probleme, die in einer Garage mit billigen Alltagsmaterialien erforscht werden können, wie auch in unserem Experiment“, so der Wissenschaftler. „Das Wichtigste ist es, neugierig zu sein und die richtigen Fragen zu stellen.“
(University of California, San Diego, 04.10.2007 – NPO)