Geheimnisvoller Gleichtakt: Forscher haben das gut 350 Jahre alte Rätsel der synchronen Pendel gelöst. Demnach sorgen weder Zufall noch geisterhafte Kräfte dafür, dass nebeneinander aufgehängte Pendeluhren nach einer Weile im Gleichtakt schwingen. Stattdessen beeinflussen sich die Uhren gegenseitig durch für uns unhörbare Schallimpulse, wie die Forscher im Fachmagazin „Scientific Reports“ berichten.
Darüber rätselte schon der holländische Physiker Christiaan Huygens: Vor gut 350 Jahren hatte er eine spezielle Box mit zwei Pendeluhren konstruiert, die auf Schiffen die genaue Zeit anzeigen sollten. Zwei Uhren deshalb, damit mindestens eine weiterlief, falls eine kaputtging. Doch beim Beobachten der nebeneinander an einem Holzbalken aufgehängten Uhren fiel ihm etwas Seltsames auf: Egal in welcher Position die Pendel starteten, spätestens nach einer halben Stunde schwangen sie komplett synchron – entweder genau in Phase oder entgegengesetzt.
Ein Fall gelöst, einer weiter offen
Diese Huygens-Synchronisation, die auch bei Metronomen funktioniert, sorgte Jahrhunderte lang für Rätselraten. Denn den naheliegenden Grund – Luftbewegungen – konnte schon Huygens selbst entkräften. 2002 gelang es Wissenschaftlern, zumindest einen Teil des Rätsels zu lösen: In Huygens‘ Versuchsaufbau war es der Holzbalken, der für die Synchronisation der beiden Uhrenpendel sorgte. Denn er übertrug Schwingungen von einer Uhr zur anderen, die ihr Pendeln beeinflusste.
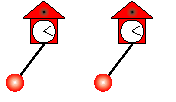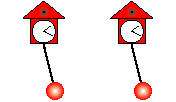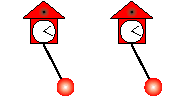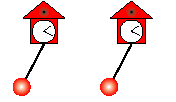
Doch eine Frage blieb ungeklärt: Warum auch Uhren synchron pendeln, die an einer Wand aufgehängt sind – also ohne „Überträger“-Balken oder sonstige Möglichkeit, Schwingungen auszutauschen. Henrique Oliveira von der Universität Lissabon und seine Kollegen haben sich diesen Fall nun vorgenommen. Mit Hilfe eines Experiments und eines Modells kamen sie dem Rätsel der Synchronisation auf die Spur.
