Ein internationales Mathematikerteam hat einen neuen Rekord in einem antiken Mathematikproblem aufgestellt. Sie berechneten so genannten kongruenten Zahlen für die Fläche rechtwinkliger Dreiecke bis zu einer Billion. Ausschrieben würde die resultierende Zahlreihe bis zum Mond und zurück reichen.
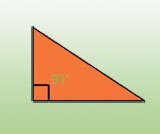
Das Problem, das zum ersten Mal vor mehr als tausend Jahren gestellt wurde, betrifft die Flächen von rechtwinkligen Dreiecken. Es ist überaschend schwer zu bestimmen, welche ganzzahligen Werte die Fläche in einem Dreieck einnehmen kann, dessen Seitenlängen ebenfalls ganze Zahlen oder Brüche sind. Die Fläche in einem solche Dreieck wird als kongruente Zahl bezeichnet. So hat ein rechtwinkliges Dreieck der Seitenlängen 3-4-5 die Fläche von 1/2x3x4=6. Die kleinste kongruente Zahl ist 5, die Fläche eines Dreiecks mit den Seitenlängen 3/2, 20/3 und 41/6.
Jahrhundertelang war es Ziel von Mathematikern, die Reihe der möglichen kongruenten Zahlen möglichst weit zu verlängern. Bekannt war beispielsweis schon, dass in der Reihung 5, 13, 21, 29, 37, …, alle Zahlen eine kongruente Zahl darstellen. In anderen, ähnlich aussehende Reihen wie 3, 11, 19, 27, 35, …., dagegen nicht. „Alte Probleme wie dieses mögen obskur erscheinen, aber sie bewirken eine Menge interessante und nützliche Forschung, während Leute neue Wege entwickeln um sie zu lösen“, erklärt Brian Conrey, Lieter des American Institute of Mathematics.
Jetzt hat ein internationales Forscherteam mit Mathematikern aus Europa, Australien, Nord- und Südamerika erstmals die kongruenten Zahlen für rechtwinklige Dreiecke bis zu einer Billion berechnet. Sie kamen auf 3.148.379.694 Fälle.
„Der schwierige Teil war die Entwicklung einer schnellen allgemeinen Bibliothek von Computercode um diese Art von Berechnungen druchzuführen“, erklärt Teammnitglied Bill Hart von der Warwick Universtität in England. „Als wir das einmal hatten, dauerte es nicht mehr lange um das spezialisierte Programm zu schreiben, das für diese spezielle Kalkulation gebraucht wurde.“ Die Mathematiker nutzten als Basis für ihre Programm frei erhältliche Software – im Prinzip könnte jeder mit einem größeren Computer daher ihre Berechnung nachvollziehen oder übertreffen.
Um sicherzugehen, dass ihre Ergebnisse stimmen und sich keine Fehler in die Programmierung oder Formeln der Berechnung eingeschlichen haben, führten die Mathematiker die gesamte Prozedur zweimal auf unterschiedlichen Computern mit verschiedenen Algorithmen und von verschiedenen Forscher geschrieben, durch. Beide Ergebnisse stimmten überein.
(American Institute of Mathematics, 23.09.2009 – NPO)