Überraschende Entdeckung: Die Kreiszahl Pi versteckt sich sogar im Wasserstoff-Atom, wie Forscher durch Zufall entdeckten. Sie stießen auf die klassische Formel für die Kreiszahl als Produkt mit unendlich vielen Faktoren, als sie Abweichungen bei der Berechnung der Energiezustände des Wasserstoffs ermittelten. Damit lässt sich diese gut 300 Jahre alte Formel für Pi erstmals direkt aus der Quantenphysik ableiten.
Pi steckt überall: In jedem runden Gegenstand, aber auch in jeder Schwingung und Welle ist die Naturkonstante Pi enthalten. Sie beschreibt nicht nur das Verhältnis vom Umfang eines Kreises zu seinem Durchmesser, sondern mischt auch bei vielen physikalischen Phänomenen mit – vom Verhalten von Wellen bis zur Heisenbergschen Unschärferelation. Insofern erscheint die Entdeckung von Pi in den Energieniveaus des Wasserstoffs erst einmal wenig ungewöhnlich. Denn letztlich geht es dabei um Elektronenbewegungen um den Atomkern.
Doch das Besondere ist in diesem Fall nicht die Kreiszahl an sich, sondern die Art, wie sie in der quantenmechanischen Formel auftaucht. „Wir haben nicht einfach Pi entdeckt,“, erklärt Tamar Friedmann von der University of Rochester. „Wir haben die klassische Wallis-Formel aus dem 17. Jahrhundert darin gefunden – zum ersten Mal überhaupt bei einem physikalischen Phänomen.“
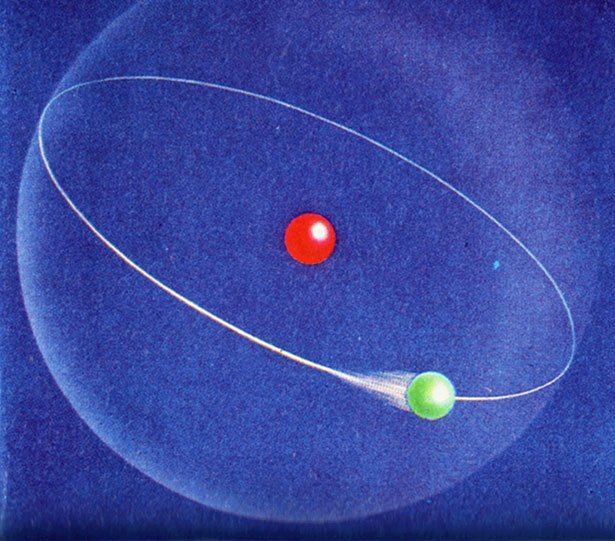
Wasserstoff und Energiezustände
Mit der Wallis-Formel versuchte der englische Mathematiker John Wallis 1655, die Kreiszahl Pi in mathematisch zu erfassen. Seine Formel definiert Pi als Produkt mit unendlich vielen Faktoren. Eine solche Abfolge von Faktoren entdeckten auch Friedman und sein Kollege Carl Hagen, als sie ihre Studenten die Energiezustände des Wasserstoffatoms berechnen ließen.
Mit einer von Niels Bohr entwickelten Formel geht dies bei diesem Atom normalerweise sehr genau, doch die Forscher ließen ihre Studenten eine alternative Rechenmethode ausprobieren, das sogenannte Variationsprinzip. Dieses nutzt man, um nicht genau bestimmbare Energiezustände mathematisch einzugrenzen und so zu schätzen. Durch Vergleich mit den Ergebnissen der Bohrschen Formel konnten die Studenten den jeweiligen Schätzfehler für jedes Niveau genau bestimmen.
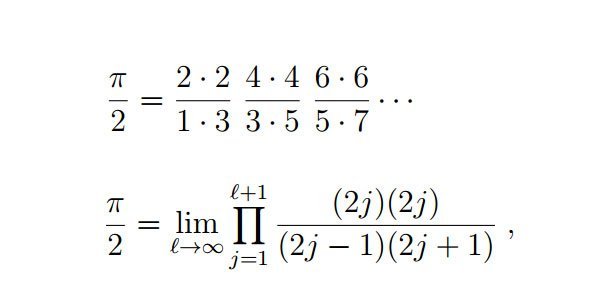
Abweichungsmuster ergibt Pi
Dabei fiel den Forschern etwas Ungewöhnliches auf: Die Abweichungen des Variationsprinzips betrugen 15 Prozent für den Gundzustand des Wasserstoffs, zehn Prozent für den ersten Anregungszustand und wurden dann immer kleiner, je stärker angeregt das Atom war. Als Hagen und Friedman diese Abweichungen in einer Formel beschreiben wollten, stießen sie auf die Wallis-Formel für Pi.
„Das war eine vollkommene Überraschung! Ich bin vor Aufregung auf und ab gesprungen“, berichtet Friedman. „Es ist faszinierend, wie eine rein mathematische Formel aus dem 17. Jahrhundert ein physikalisches System beschreibt, dass erst 300 Jahre später entdeckt wurde.“ Sein Kollege Hagen ergänzt: “ Mich hat überrascht, dass die Formel in einer so natürlichen Art bei den Berechnungen auftauchte, obwohl bei der Bestimmung der Energiezustände gar keine Kreise involviert waren. Wir haben gar nicht nach Pi gesucht, es fiel uns einfach in den Schoß. (Journal of Mathematical Physics, 2015; doi: 10.1063/1.4930800)
(University of Rochester, 11.11.2015 – NPO)